#4. 기계학습 수학2
평균 μμ와 분산 σ2σ2으로 정의다차원 가우시안 분포 ; 평균벡터 μμ와 공분산행렬 ΣΣ로 정의ㅇUpdate Log
| 22.09.20 First Update
| 22.10.12 Second Update
이번 시간에는 기계학습에서 사용되는
확률과 통계에 대해서 알아보겠다.
기계학습이 처리할 데이터는 불확실한 세상에서 발생하므로,
불확실성을 다루는 확률과 통계를 잘 활용해야 한다.
확률 기초
확률변수 ( Random Variable)
윷놀이에 대해서 생각해보자

- 이 윷놀이에서 나올 수 있는 5가지의 경우중에서
- 한 값을 가지는 확률변수를 x라고 하자
- 이때 x의 정의역은 {도, 개, 걸, 윷 모} 이다.
확률분포
위의 나왔던 윷놀이의 예시를 확률분포로 표현해보자.

- 이때 우리가 이산인 경우와 연속인 경우로 나눌 수 있다.
- 이산인 경우에는 확률 질량 함수로 나타낸다.
- 연속인 경우에는 확률 밀도 함수로 나타낸다.
확률 벡터
- 확률 벡터와 같은 경우에는 예시를 들어보자.
- 앞에서 계속 봐왔던 데이터셋에서 Iris 데이터 셋을 생각해보자
- 이때 Iris 데이터 셋에서 확률 벡터 x를 다음과 같이 표현할 수 있다.

용어에 대한 정의는 이쯤 하고
더 정확한 식을 유도하기 위해서
간단한 확률 실험장치를 생각해보자.
가정은 다음 2가지가 있다고 생각하자
1) 주머니에서 번호를 뽑은 다음, 번호에 따라 해당 병에서 공을 뽑고 색을 관찰한다.
2) 번호를 y, 공의 색깔을 x라는 확률 변수로 표시하자.


합 규칙과 곱 규칙

- 곱 규칙은 다음과 같다.
- 위에 예시를 적용한다면 다음과 같은 식이 나온다.
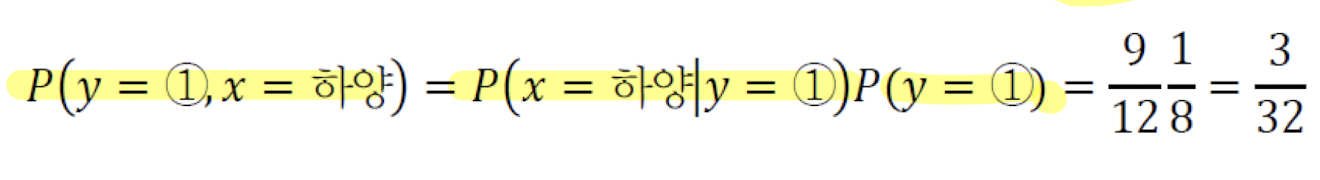

- 합규칙은 다음과 같다.
- 위의 예시를 적용한다면 다음과 같은 식이 나온다.
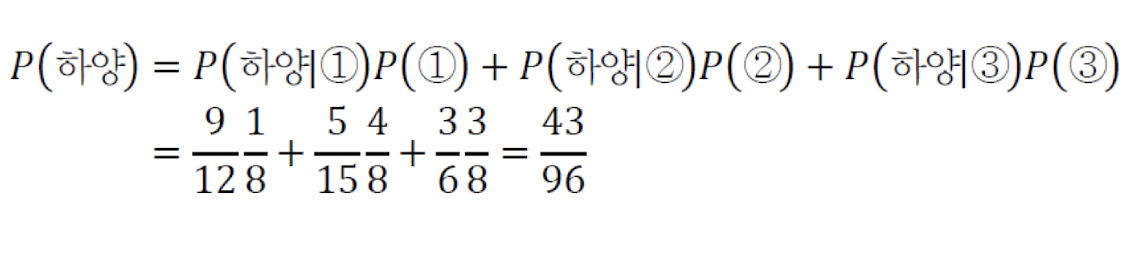
베이즈 정리와 기계학습
위의 식들을 융합한 게 아래 베이즈 정리의 식과 같다.

예시를 들고 한국말로 풀었을 때는
"하얀 공이 나왔다는 사실만 어느 병에서 나왔는지 모르는데, 어느 병인지 추정하라"
위의 말을 식으로 표현하면 다음과 같다.
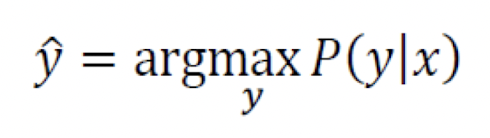
위의 식과 베이즈 정리를 융합하면 다음과 같다.

이를 풀면 다음과 같은 식으로 쓸 수 있다

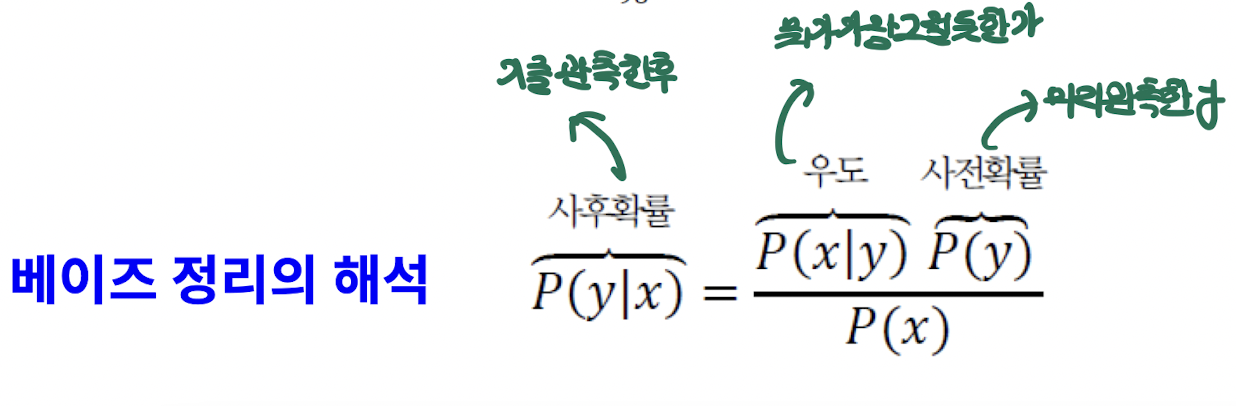
- 사후 확률
- x를 관측한 후
- 우도
- 뭐가 가장 그럴듯한가
- 사전 확률
- 미리 관측한 y
그렇다면 이것을 기계학습에 적용하려면
어떻게 해야 할 것인가?
우리가 들었던 Iris 데이터셋에서 예시를 또 들어보면 다음과 같다.

- 우도확률은 밀도추정 기법으로 추정 정리하자면
- 기계학습에서 사후확률로 문제를 풀고 싶어하는것이 목적이다.
- 이때 사후확률을 직접적으로 푸는 것이 불가능하다.
- 따라서 사전확률과, 우도를 통해서 푸는 것이다.
최대 우도
매개변수 를 모르는 상황에서 매개변수를 추정하는 문제이다.

- 이때 최대 우도는 그중에서 가장 그럴듯한 애를 찾는 과정이다.

그래서 이 경우에 수식으로 쓰면

- 이때 P(X|q3)와 같은 경우는
- "X가 나올 가능성이 제일 큰 q3의 값을 찾아라" 라는 뜻이다.
- 또한 이 식을 모든 문제에 적용하기 위해서 일반화를 한다면 다음과 같다.
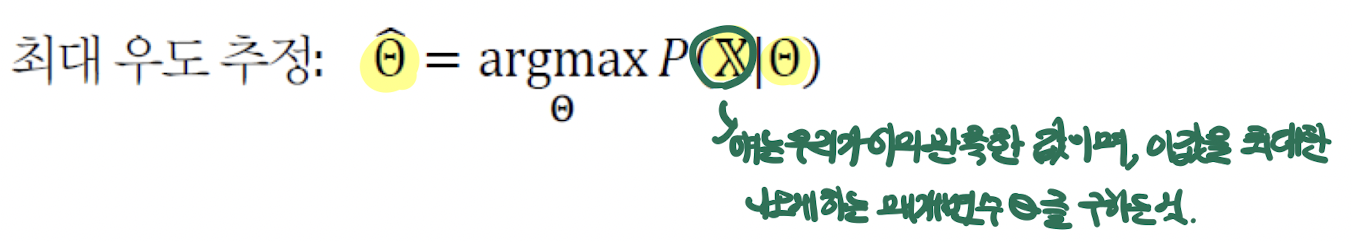
- 이때 쓰여 있듯이 X는 이미 우리가 관측한 값이다.
- 이 값을 최대한 나오게 하는 매개변수 ''를 구하는 것이다.
- 이 식을 계속 나열하면서 곱하다 보면, 확률 값이라서 굉장히 작아지게 된다.
- 이를 피하기 위해서 '로그' 계산을 시도하게 되는데 ,이때 우리는 최대 로그 우도 추정이라고 부른다.

평균과 분산
우리는 데이터의 요약적인 정보로서
평균과 분산을 사용하게 된다.
앞으로 우리가 쓰게 될 식은 2개 다음과 같다.
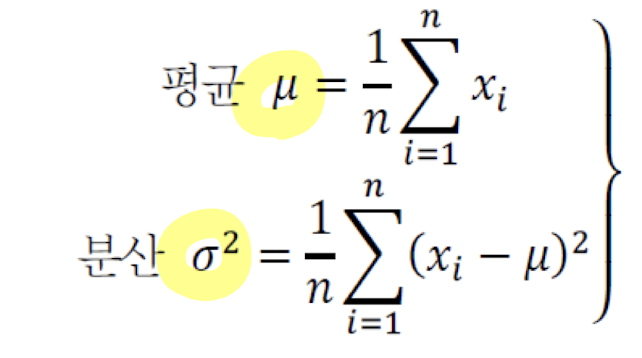
- 이때 분산이 크다는 의미
- 평균보다 값이 멀어져 있다는 뜻이다.
- 또한 분산이 작다는 의미
- 평균 근처에 값이 모여져 있다는 뜻이다.
- 데이터가 1차원이 아니라 다차원일 때
- 우리는 벡터와 행렬을 통해서 평균과 분산을 표현한다.
- 이때 사용되는 개념이 평균 벡터와 공분산 행렬이다.
- 평균벡터
- 치우침의 정도
- 공분산행렬
- 확률변수의 상관정도

유용한 확률분포
가우시안 분포
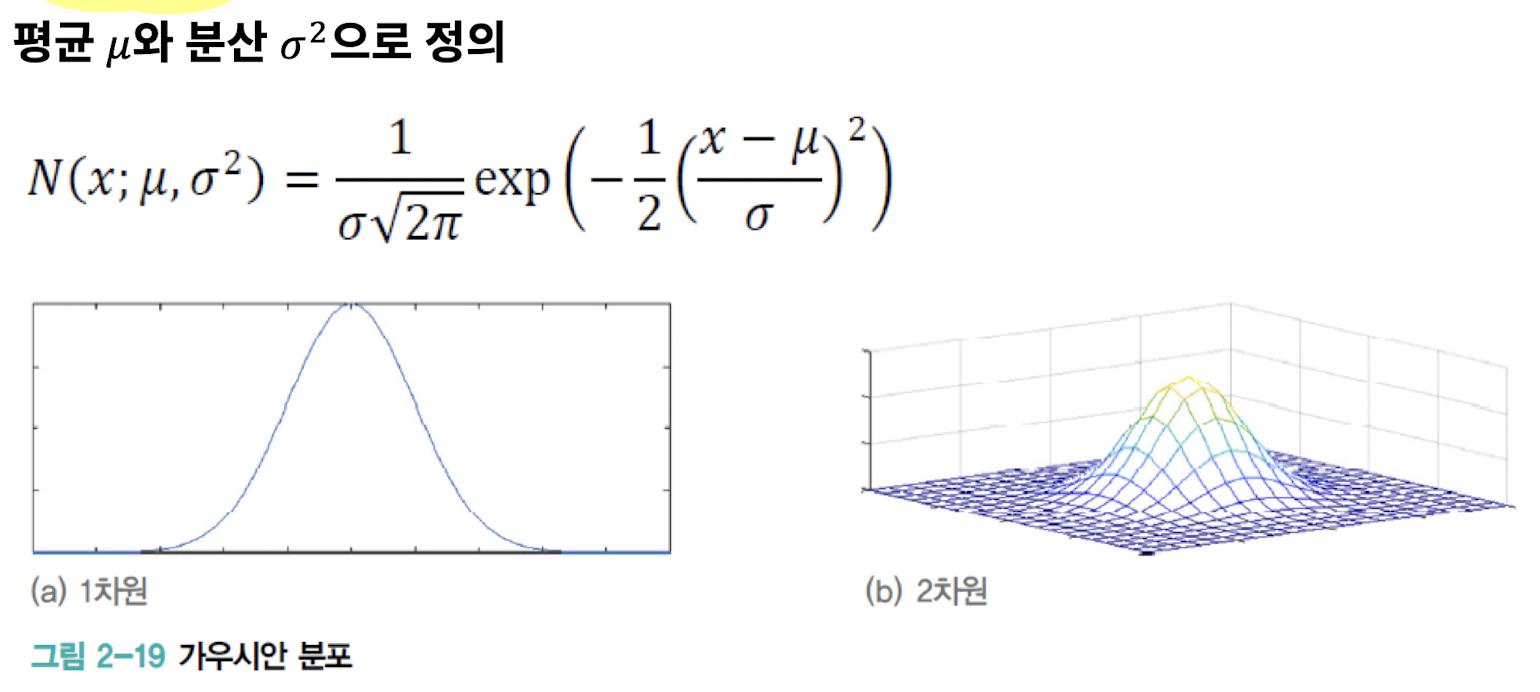
- 평균 와 분산 으로 정의
- 다차원 가우시안 분포
- 평균벡터 와 공분산행렬 Σ로 정의
베르누이 분포

이항 분포

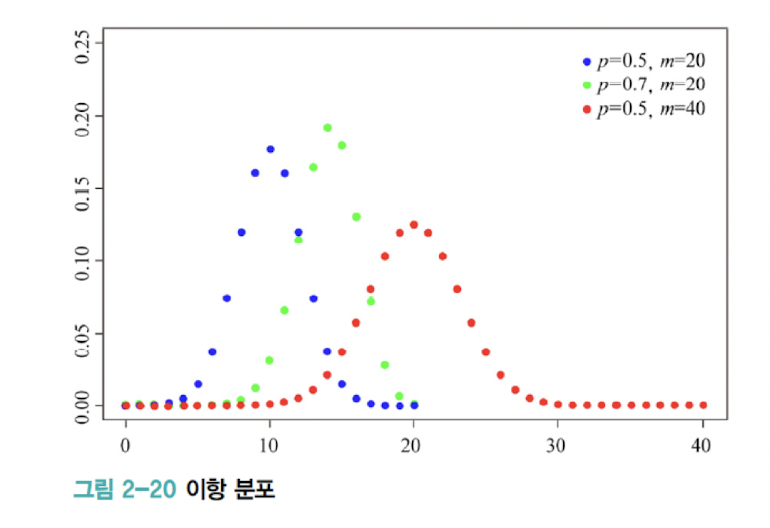
정보 이론
메시지가 지닌 정보를 수량화할 수 있을까?
예를 들어서 "고비사막에 눈이 왔다"와
"대관령에 눈이 왔다"라는 두 메시지 중 어느 것이 더 많은 정보를 가질까?
정보이론의 기본원리는
확률이 작을수록 많은 정보
즉, 희귀할수록 많은 정보를 가지고 있다는 것이다.
- 정보이론 관점에서도 기계학습을 접근이 가능하다.
- 불확실성을 정량화 하여, 정보이론 방법을 기계학습에 활용할 수 있다.
- ex) 엔트로피, 교차 엔트로피, KL 다이버전스
- 정보이론
- 사건 (Event)가 지닌 정보를 정량화 할 수 있나?
- 우리는 이를 불확실성을 통해서 정량화 한다.
- 불확실성이은 확률적으로 작게 일어나는 것이다.
자기 정보 (Self Information)
- 사건 (메시지) ei의 정보량 (단위: 비트 또는 나츠)

(여기서 표현되는 비트는 우리가 아는 그 비트가 맞다.)
- 이때 두 가지의 정보량을 비교하는 기준은 밑이 2인지 e 인지에 따라 다르다
- 로그의 밑이 2인경우: 비트 (bit)
- 로그의 밑이 e인경우: 나츠 (nat)
- 이 자기정보 값이 높을수록 높은 정보량을 가진다.
- 확률변수 하나 (즉, 이벤트 하나)만 보는 것이 자기 정보이다.
엔트로피
- 엔트로피의 정의
- 확률변수 x의 불확실성을 나타내는 량이다.
- 이때 확률변수 하나만 보는 것이 아니라 확률변수가 가질 수 있는 모든 사건의 불확실성을 나타내는 것이 엔트로피이다.
- 같은 말이지만 확률변수가 얼마나 불확실 한가, 같은 말로는 정보량의 기댓값이라고 할 수 있다.
- 이때 엔트로피는 이산확률분포일 때와 연속확률 분포 일때 식이 다르다.

예제를 보면서 이해해보자.

이때 이렇게 나와 있을 때 주사위가 윷보다 엔트로피가 높은 이유는?
- 주사위는 모든 사건이 동일한 확률을 가진다.
- 즉 어떤 사건이 일어날지 윷보다 예측이 어렵다.
- 주사위가 윷보다 더 무질서하고 불확실성이 크다.
- 즉 주사위가 윷보다 엔트로피가 높다.
교차 엔트로피 (Cross Entropy)
- 두 확률분포 P와 Q 사이의 교차 엔트로피라고 부르는 것이 정확하다.
- 심층학습에서의 손실 함수에 자주 사용한다.
- 예측값과 실제값 둘의 확률분포가 얼마나 서로 공유하는지를 척도로 나타낼 수 있다.


- 여기에서 P를 데이터의 분포라고 하자.
- P는 학습과정에서 변화하지 않는다.
- 즉 P 의 값은 고정이고 , Q의 값을 조정시켜서 P에 대해서 맞춘다.
- 교차 엔트로피를 손실함수로 사용하는 경우
- 이는 KL 다이버전스의 최소화함과 동일하다.
- 즉 Q 를 조정해서 손실함수를 최소화 함이다.
KL 다이버전스

- 두 확률분포 사이의 거리를 계산할때 주로 사용한다.
- 확률분포 Q를 움직여서 움직이지 않는 데이터 확률분포 P와 비슷하게 맞춰주는 것이다.
교차 엔트로피와 KL 다이버전스의 관계

- 즉, 가지고 있는 데이터 분포 P(x) 와 추정한 데이터 분포 Q(x)간의 차이를 최소화하는데 교차 엔트로피를 사용
'STUDY > 인공지능' 카테고리의 다른 글
| #6. 다층 퍼셉트론 및 딥러닝 기초 (0) | 2022.11.01 |
|---|---|
| #5. 최적화 이론 (1) | 2022.11.01 |
| #3. 기계학습 수학 1 (0) | 2022.11.01 |
| #2. 기계학습 복습 2 (1) | 2022.11.01 |
| #1. 기계학습 복습 1 (1) | 2022.11.01 |









